PCA против ICA: разница? – Технология с технологией

Вот все о разнице между PCA и ICA:

PCA пытается найти взаимно ортогональные компоненты, тогда как в ICA компоненты могут не быть ортогональными.

ICA ищет взаимно независимые компоненты. PCA пытается максимизировать дисперсию входного сигнала вместе с основными компонентами, в то время как ICA минимизирует взаимную информацию в найденных компонентах.

Так что если вы хотите узнать все о том, чем именно отличаются PCA и ICA, то вы попали по адресу.

Давайте погрузимся прямо в!

Каковы основы PCA и ICA?

PCA (анализ основных компонентов) и ICA (анализ отдельных компонентов) основаны на схожих принципах, но все же они разные.

Сразу разобраться во всех формулах, приведенных при описании методов PCA и ICA, непросто.

Математика — красивая наука, но чтобы понять эту красоту, нужно идти шаг за шагом — прыгнуть сразу на несколько шагов почти невозможно.

Часто необходимо сначала исследовать тот или иной метод на простом примере, чтобы в голове сложилась картина, которую можно распространить на более сложные случаи.

Это особенно верно в случае многомерных пространств, таких как концепции PCA и ICA.

Человеческий мозг не может представить n-мерное пространство для n > 3.

Мы рассмотрим простые примеры приложений PCA и ICA и попытаемся понять основные принципы, лежащие в основе этих методов.

Начнем с постановки задачи для ППШ:

Что такое PCA и как его реализовать в Python?

Если мы говорим об анализе данных, то, скорее всего, вы будете использовать многомерные массивы признаков.

Такие массивы, кстати, называются тензорами.

Часто бывает, что размерность этих данных избыточна. Например, одна величина может напрямую зависеть от другой.

Допустим, вы можете рассчитать квадратные метры квартиры из квадратных метров квартиры.

Это означает, что нам не нужно использовать оба этих значения в анализе; вы можете отбросить одно из значений (квадратные метры или квадратные метры) в вашем анализе.

В этом случае корреляция между значениями равна единице; это означает, что они строго связаны.

Но могут быть и более слабые связи, например, время разгона автомобиля от 0 до 100 кмч зависит от объема двигателя, но напрямую его не определяет.

Есть и другие факторы, такие как вес и аэродинамика автомобиля, конструкция двигателя и многое другое.

Если мы знаем точные формулы зависимостей, то можем уменьшить количество оцениваемых факторов и объединить их в один.

Но, конечно, чаще всего эти зависимости не столь очевидны и их сложно найти.

Тем не менее, некоторые методы могут уменьшить размер массива признаков для анализа.

Одним из таких методов является ПКА.

Он позволяет выбрать компоненты из массива признаков и оценить, как тот или иной компонент влияет на то, насколько сильно будут отличаться друг от друга реальные объекты, описываемые изучаемыми признаками.

Давайте рассмотрим синтетический пример, который покажет, как работает PCA.

Может быть много разных реализаций PCA.

Мы будем моделировать самый простой.

Для начала возьмем два значения, они будут зависеть друг от друга линейно, но дополнительно введем небольшой случайный шум.

Давайте также стандартизируем значения.

Вычтите ожидаемое значение из каждого значения и разделите на стандартное отклонение:

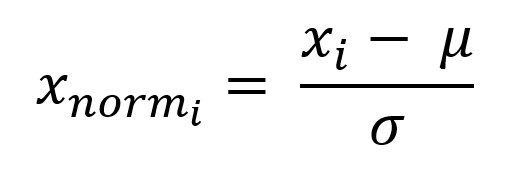
%matplotlib встроенный импорт matplotlib.pyplot as plt import sklearn.decomposition as deco plt.style.use(‘seaborn-whitegrid’) import numpy as np x = np.linspace(1, 30, 100) y = x + np.random .randn(100) xnorm = (x – np.mean(x)) / np.std(x) ynorm = (y – np.mean(y)) / np.std(y) X = np.vstack(( хнорм, инорм))

Перенесем точки на график:

plt.plot(X[0]ИКС[1]”о”)

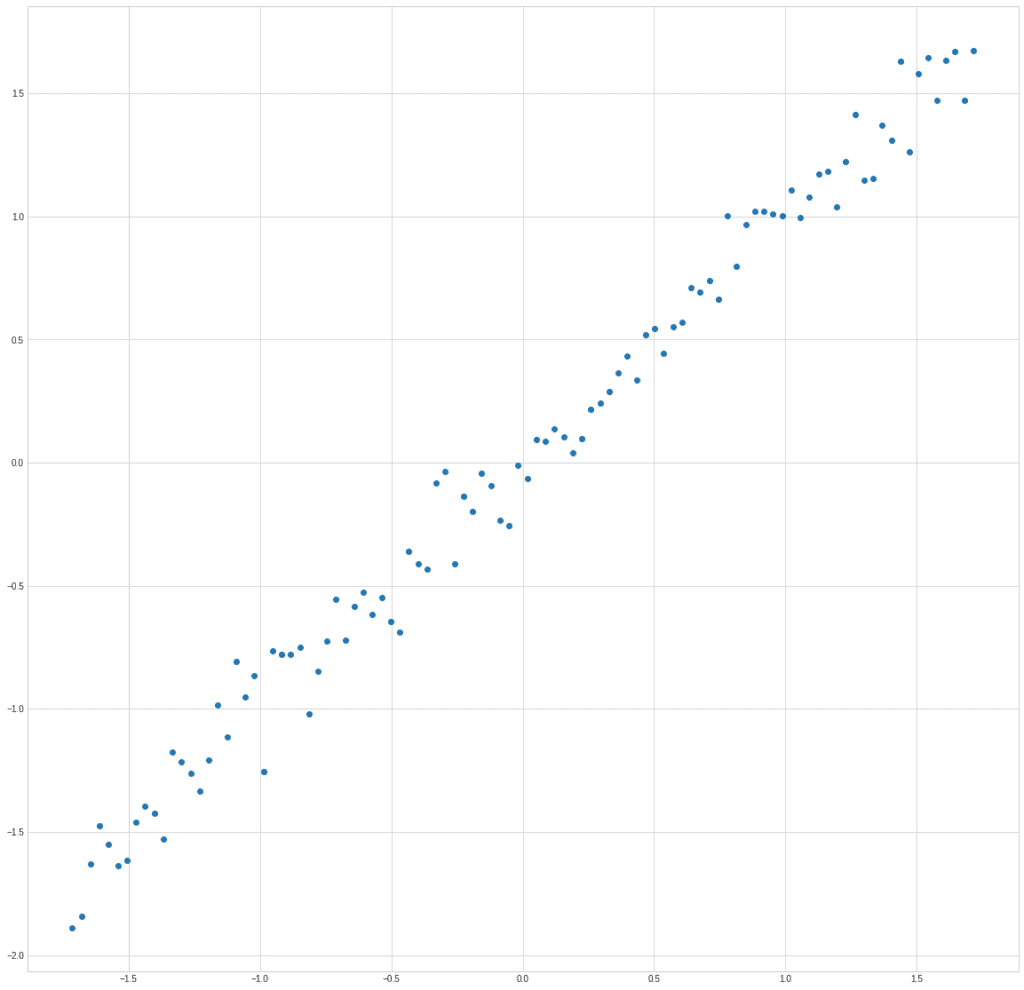
На графике хорошо видно, что именно мы заложили в структуру данных, зависимость параметра y от x:

plt.plot(X[0]ИКС[1]”о”) plt.plot([-2,2], [-2,2])

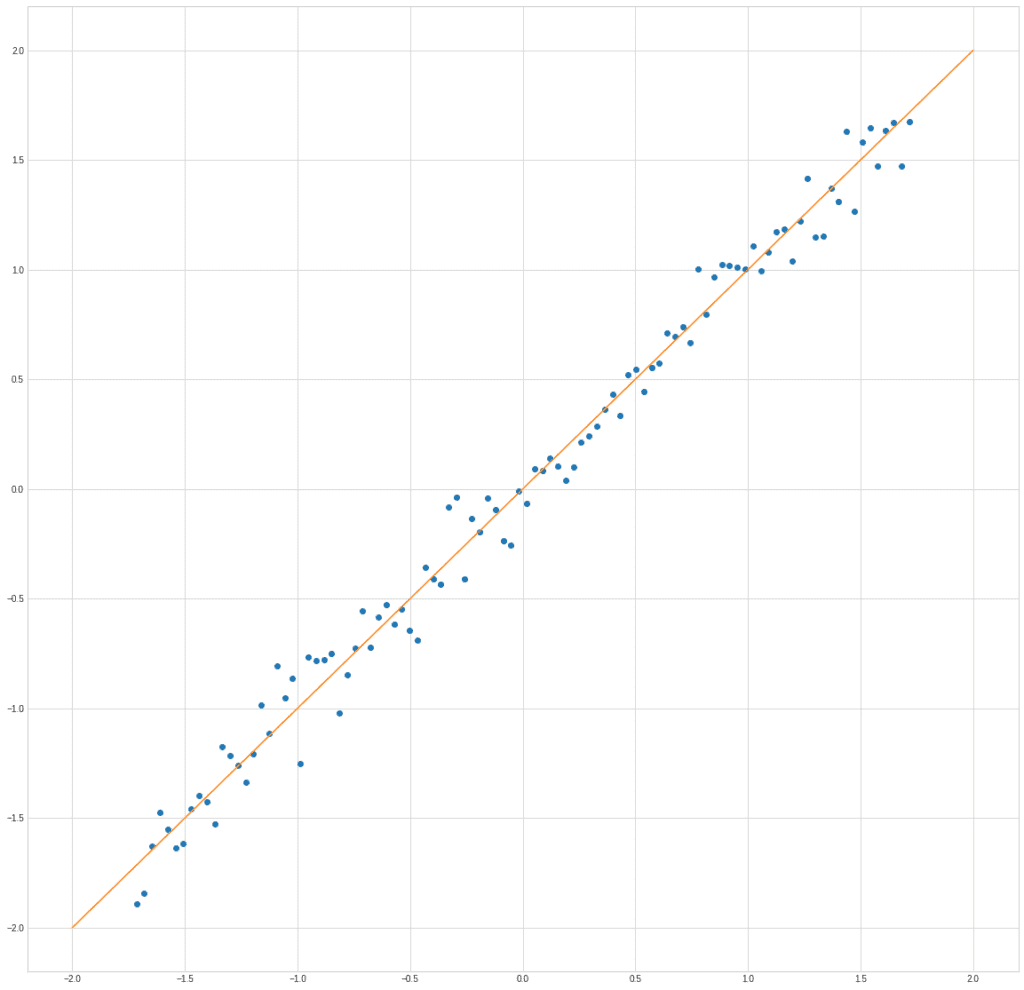
С помощью PCA мы можем найти новую черту, которая будет комбинацией этих двух.

Естественно, при замене двух признаков на один часть информации будет утеряна.

Задача алгоритма состоит в том, чтобы минимизировать эти потери.

В этом случае, очевидно, можно использовать проекцию точек на прямую x1 = x2.

Именно вдоль этой линии разброс данных максимальный.

Мы используем ковариационную матрицу для оценки зависимости двух векторов.

Ковариация обычно определяется как мера зависимости от двух случайных величин:

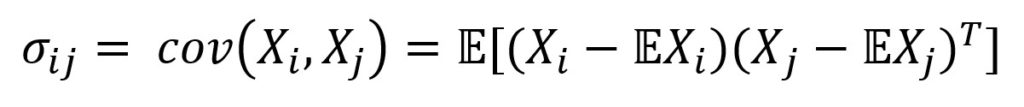
Где E — оператор ожидания. Итак, мы центрируем векторы — вычитаем математическое ожидание вектора из каждого значения, а затем находим их внутренний продукт.

Скалярное произведение в евклидовом пространстве определяется как произведение длин векторов на косинус угла между ними.

Если векторы ортогональны, то косинус угла будет равен 0.

Соответственно, вычисляя скалярное произведение, мы ищем, насколько векторы не совпадают по направлению.

Дисперсии соответствующих значений расположены вдоль главной оси ковариационной матрицы. В питоне легко найти ковариационную матрицу.

Для знаков это будет так:

ковариация = np.cov(X) print(ковариация)
[[1.01010101 1.00366207]
[1.00366207 1.01010101]]

Как будет выглядеть ковариационная матрица?

Это будет смотреться диагонально.

Кроме главной диагонали, остальные значения будут равны нулю.

Мы как раз пытаемся найти такой базис, то есть нам нужно диагонализовать ковариационную матрицу.

Это легко сделать с собственное разложение.

Мы можем представить любую квадратную матрицу линейно независимых строк как:

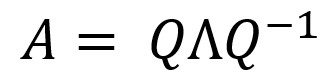
Где Вопрос — матрица, состоящая из собственных векторов, и л диагональная матрица, элементы которой вдоль главной диагонали равны собственным значениям матрицы Аа остальные элементы равны 0.

Таким образом, для нахождения нового базиса — векторов, вдоль которых зависимость будет минимальной, необходимо найти собственные векторы ковариационной матрицы.

И это также легко сделать с модулем NumPy:

собственные значения, собственные векторы = np.linalg.eigh (ковариация) печать (собственные векторы) печать (собственные значения)
[[-0.70710678 0.70710678]
[ 0.70710678 0.70710678]]печать (собственные значения)
[0.00642988 2.01377214]

Сами векторы располагаются в столбцах получившейся матрицы. Выберем первый и второй собственные векторы для ковариационной матрицы:

ev1 = собственные векторы[:, 0]
ev2 = собственные векторы[:, 1]

Мы можем проверить, что они действительно являются собственными векторами по определению.

Произведение матрицы на собственный вектор должно быть равно произведению собственного значения на тот же вектор:

печать (ковариация @ ev1) печать (собственные значения[0] * ev1)
[-0.00455302 0.00455302]
[-0.00455302 0.00455302]

печать (ковариация @ ev2) печать (собственные значения[1] * ev2)
[1.42394553 1.42394553]
[1.42394553 1.42394553]

Как видите, результат идентичен.

Давайте попробуем построить векторы вместе с набором данных, чтобы убедиться, что мы действительно нашли правильные направления:

plt.plot(X[0]ИКС[1]”o”) plt.arrow(0, 0, ev1[0] * собственные значения[0] * 10, изд1[1] * собственные значения[0] * 10, цвет = “r”, ширина = 0,01) plt.arrow(0, 0, ev2[0] * собственные значения[1]ev2[1] * собственные значения[1]цвет = “b”, ширина = 0,01) plt.show()

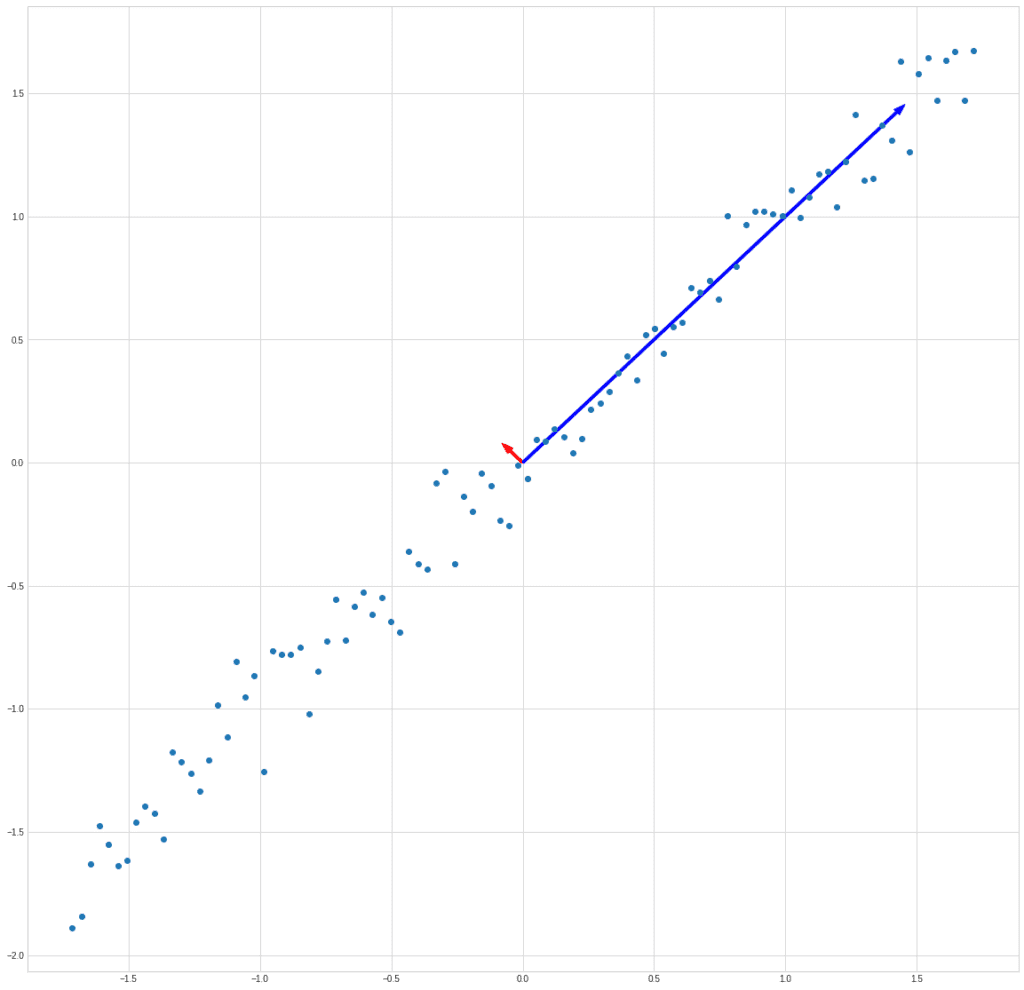
Рисуем векторы не в масштабе, потому что собственные значения в примере отличаются на 4 порядка.

Но мы видим, что у нас получилось два ортогональных вектора, один из которых направлен в сторону максимальной зависимости, а другой перпендикулярен ей.

Чтобы получить новые значения координат, нам просто нужно умножить матрицу собственных векторов на исходную матрицу признаков:

X_new = собственные векторы @ X

Теперь давайте найдем стандартное отклонение двух новых функций:

печать (np.std (X_new[0])) печать (np.std (X_new[1])) 0,07984079617577441 1,4119580189460372

Стандартное отклонение по оси красного вектора в 17 раз меньше, чем по синему. Мы можем отказаться от всего столбца и использовать только один X_новый [1] вместо двух функций х1 и х2.

На деле получается, что мы заменяем синие точки на зеленые:

plt.plot(X[0]ИКС[1]”о”) plt.plot([-2,2], [-2,2]) plt.plot(X_new[1] / np.sqrt(2), X_new[1] /np.sqrt(2), “о”)

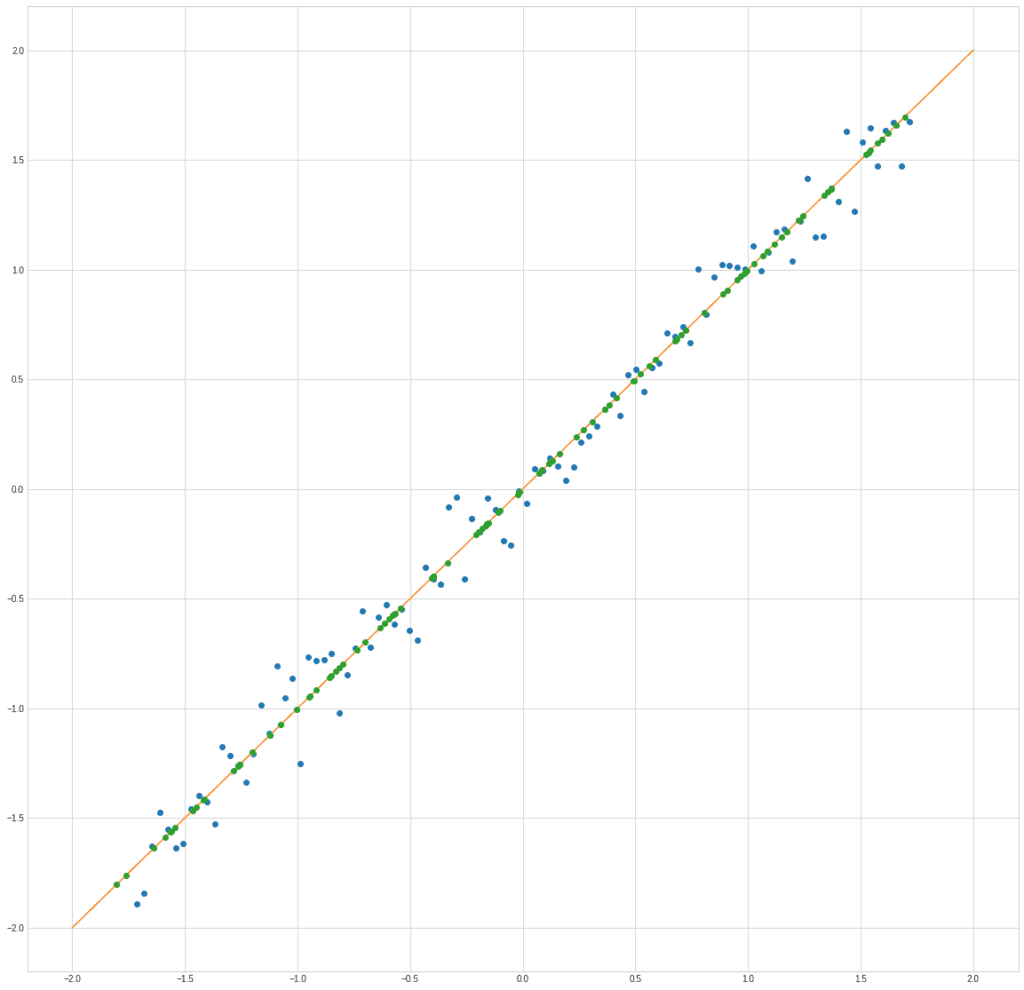
Потери, конечно, есть, но во многих случаях ими можно пренебречь.

Можно рассчитать потерю информации, оценив соотношение оставшихся собственных значений и тех, которые мы отбрасываем.

В общем, PCA позволяет преобразовать n признаков в мгде м << п.

Для практических задач удобнее использовать готовые реализации.

Например, мы можем взять модель PCA из модуля sklearn.decomposition:

из sklearn.decomposition import IncrementalPCA X = np.stack((xnorm, ynorm), ось = 1) pca = deco.PCA(1) xt = pca.fit_transform(X) print(xt.shape) (100, 1)

Мы передаем один параметр в деко.PCA функция—мновое количество функций, которые мы хотим сохранить.

На выходе получаем массив новых фич, часть которых автоматически отбрасывается в соответствии с заданным параметром.

Мы можем сравнить признаки, вычисленные методом, и готовую функцию из научился:

printzip(* (xt.reshape(100), X_new[1])) (-2,378511170140015, -2,3785111701400123) (-2,4911929631729186, -2,4911929631729177) (-2,172690411576331, -2,1726904115763306 ) (-2,321844756744973, -2,3218447567449725) (-2,213965105057678, -2,213965105057677) (-2,0648350319020237, -2,0648350319020228) …

Вывод усекается до первых 6 пар чисел. Как видите, они совпадают с ошибкой округления.

Что такое ICA и как его реализовать в Python?

Чаще всего можно услышать об ICA как о способе решения проблемы слепого разделения источников.

Эта проблема также называется проблемой коктейльной вечеринки.

Представьте, что вы находитесь на вечеринке, где одновременно происходит несколько диалогов.

Вокруг достаточно шумно, но общаться с собеседником все же можно, человеческий слух и мозг успешно решают эту задачу и выделяют значимый сигнал из общего шума.

Решение этой задачи не так просто математически:

Представим, что у нас есть 3 источника сигнала и несколько микрофонов, записывающих линейную комбинацию сигналов.

Количество микрофонов должно быть не меньше количества источников сигнала. В противном случае задача будет неопределенной.

Кроме того, чтобы задача имела смысл, сигналы должны соответствовать двум требованиям:

• Источники сигнала не зависят друг от друга;
• Значения каждого из источников имеют негауссово распределение.

Источники сигналов независимы, но их смеси, конечно, не независимы, так как каждая из смесей зависит от всех источников.

Но чем больше у нас источников, тем ближе распределение каждого смешанного сигнала будет к гауссовскому.

Вот на чем основано разделение; мы попытаемся изолировать самые негауссовские компоненты от смешанных сигналов.

В любой реализации алгоритма ICA можно выделить три этапа:

• Центрирование (вычитание среднего и создание нулевого среднего для сигнала)
• Удаление из корреляции (обычно с помощью спектрального разложения матрицы)
• Уменьшение размерности для упрощения задачи

Если мы попытаемся сравнить PCA и ICA на прошлом примере, то получим примерно следующее. Возьмем смешанный сигнал:

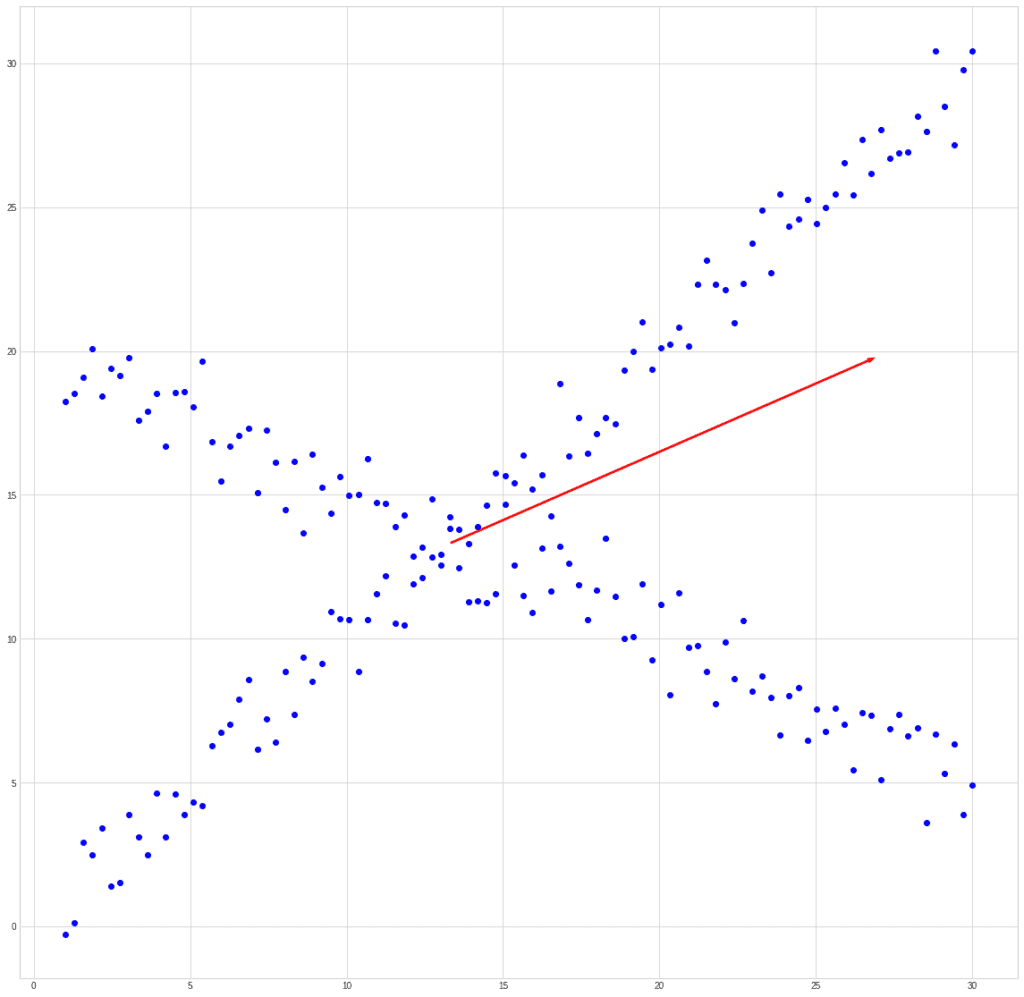
PCA найдет вектор, в направлении которого дисперсия максимальна.

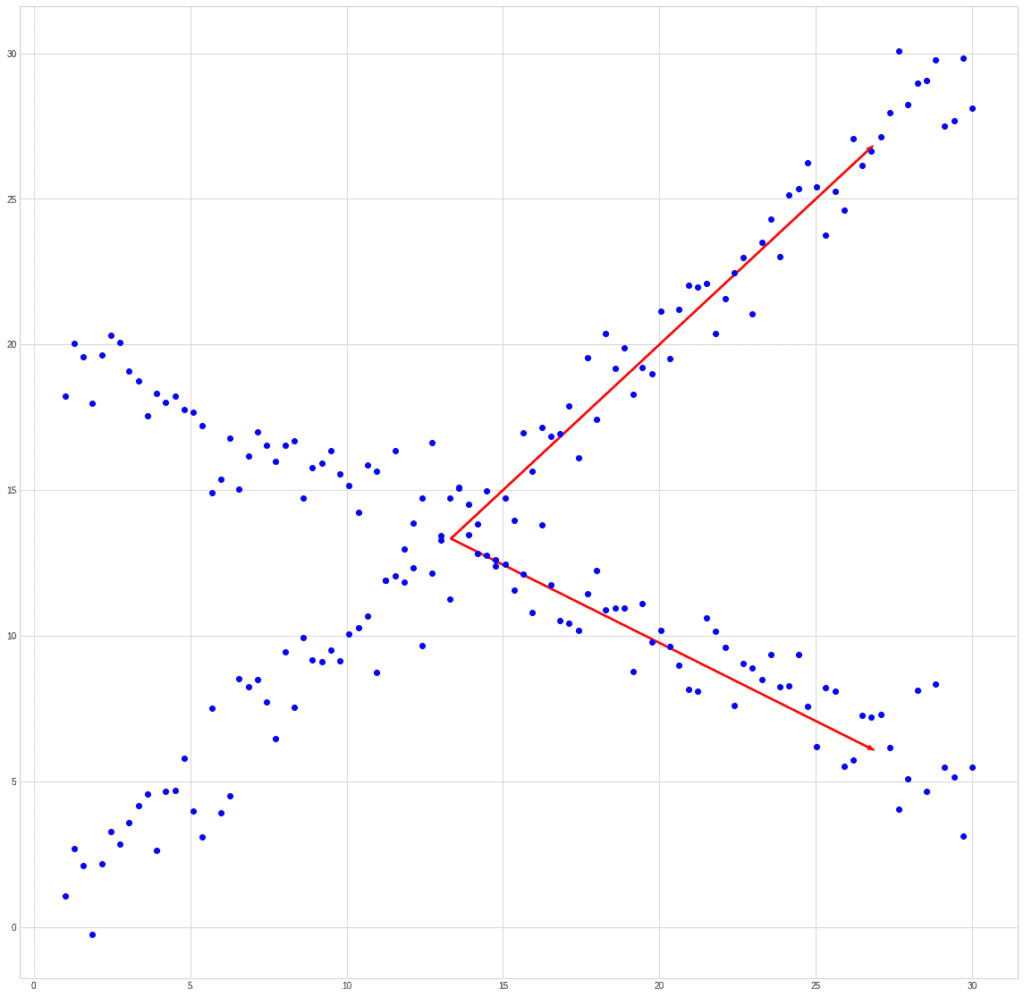
ICA найдет векторы, соответствующие смешанным сигналам.

Этот пример синтетический.

Вы должны понимать, что ограничение ICA заключается в том, что он не может восстановить порядок исходных сигналов, а также их реальную амплитуду.

Но это не проблема для таких задач, как, например, разделение аудиосигналов.

Давайте попробуем смешать и разделить два изображения из Скрыть:

из matplotlib импортировать изображение s1 = image.imread(“s1.jpg”) s2 = image.imread(“s2.jpg”) plt.imshow(s1)

plt.imshow (s2)

Создайте смешанные изображения и нормализуйте их, чтобы значения яркости оставались в диапазоне 0…255:

m1 = 0,6 * s1 + 0,4 * s2 m2 = 0,3 * s1 + 0,7 * s2 норма = лямбда x: (x * 255 / np.max(x)).astype(np.uint8) m1 = норма(m1) m2 = норма (m2) плт.imshow (m1)

plt.imshow (м2)

Как видите, эти смешанные изображения подобны тому, как если бы вы смотрели на что-то сквозь стекло и видели частично картинку за стеклом, а частично отраженное изображение.

Наша задача теперь — найти матрицу W. Такую, чтобы умножение этой матрицы на входную матрицу смешанных сигналов дало бы нам приближенно матрицу исходных независимых сигналов:

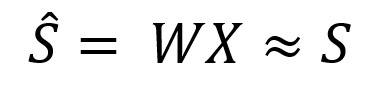
Мы можем решить эту проблему через СВД (Разложение по сингулярным значениям). Представим искомую матрицу в виде:

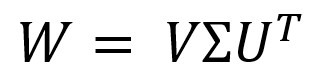
Где С представляет собой диагональную матрицу, которую можно представить в виде матрицы растяжения (масштабирования), а U и В матрицы матрицы вращения.

Таким образом вы можете написать матрицу поворота — эта матрица будет поворачивать вектор на угол я при умножении:

Таким образом, мы можем представить умножение на матрицу W в 3 этапа:

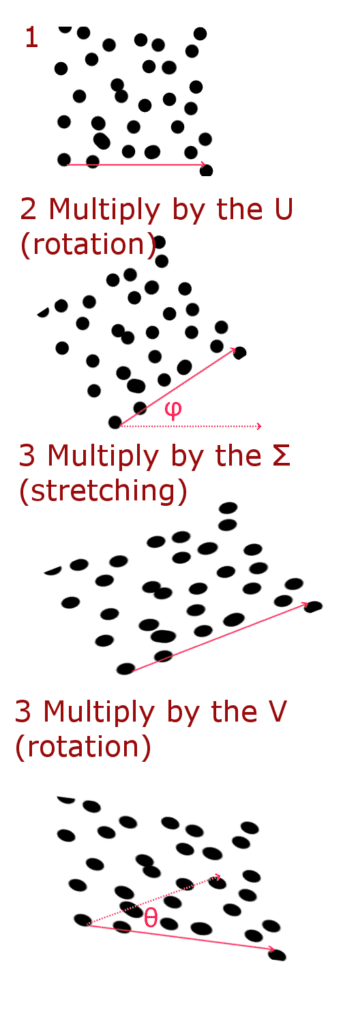
Теперь давайте реализуем это на Python. Вывод формул подробно не описывается. Вы можете увидеть их в источник.

Находить я и посмотреть его значение в градусах:

theta0 = 0,5 * np.arctan(-2 * np.sum(m1 * m2) / np.sum(m1 ** 2 – m2 **2)) theta0 * 180 / np.pi -31,781133720821153

Далее находим транспонированную матрицу U:

Нас = np.массив([ [np.cos(theta0), np.sin(theta0)], [-np.sin(theta0), np.cos(theta0)] ]) Нас массив([[ 0.85006616, -0.52667592],
[ 0.52667592, 0.85006616]])

И матрица С:

sigma1 = np.sum( (m1 * np.cos(theta0) + m2 * np.sin(theta0)) ** 2) sigma2 = np.sum( (m1 * np.cos(theta0 – np.pi/2) + m2 * np.sin(theta0 – np.pi/2)) ** 2) Sigma = np.array([ [1/np.sqrt(sigma1), 0], [0, 1/np.sqrt(sigma2)] ]) Сигма-массив([[9.39029733e-06, 0.00000000e+00],
[0.00000000e+00, 2.15484602e-06]])

Умножим смешанные сигналы на известные матрицы U и С и рассчитать угол Фи:

x1bar = сигма[0][0] * (Нас[0][0] * м1 + Нас[0][1] * м2) x2бар = сигма[1][1] * (Нас[1][0] * м1 + Нас[1][1] * m2) sum1 = np.sum(2 * (x1bar ** 3) * x2bar – 2 * (x2bar ** 3) * x1bar) sum2 = np.sum(3 * (x1bar ** 2)* (x2bar ** 2) – 0,5* (x1bar ** 4) – 0,5 * (x2bar ** 4)) tmp1 = -sum1 / sum2 phi0 = 0,25 * np.arctan(tmp1) phi0 * 180 / np.pi -1,7576366868809685

Сформируйте матрицу В:

V = np.массив ([ [np.cos (phi0), np.sin (phi0)],
[-np.sin (phi0), np.cos (phi0)] ]) Массив V([[ 0.99952951, -0.03067174],
[ 0.03067174, 0.99952951]])

Рассчитаем значения сигналов, нормализуем их и выведем изображения на экран:

s1hat = V[0][0] * x1бар + В[0][1] * x2bar s2hat = V[1][0] * x1бар + В[1][1] * x2bar s1hat = норма (s1hat).astype (np.uint8) s2hat = норма (s2hat).astype (np.uint8) plt.imshow (s1hat)

plt.imshow (s2hat)

Как видите, изображения восстановились довольно хорошо. Хотя и не идеально — вы можете видеть шум и очертания прошлых изображений.

Каковы сходства и различия между PCA и ICA?

Мы рассмотрели реализации PCA и ICA на Python.

Теперь немного о сходствах и различиях:

Сходства:

• Оба эти метода являются статистическими преобразованиями
• Оба они широко используются в различных прикладных задачах, часто даже в одних и тех же.
• Оба метода находят новые базы для представления входных данных.
• В обоих случаях мы считаем, что наблюдаемые признаки представляют собой линейную комбинацию некоторых скрытых признаков.
• Оба метода предполагают, что компоненты независимы и имеют негауссово распределение.

Отличия:

• PCA пытается найти взаимно ортогональные компоненты; в ICA компоненты могут быть не ортогональны. ICA ищет взаимно независимые компоненты
• PCA пытается максимизировать дисперсию входного сигнала вместе с главными компонентами, ICA минимизирует взаимную информацию в найденных компонентах.
• Признаки, полученные в PCA, располагаются в строгом порядке от наиболее значимых к наименее значимым. Поэтому мы можем отказаться от некоторых функций, чтобы уменьшить размерность. Компоненты, полученные в ICA, принципиально неупорядочены и эквивалентны. Мы не можем их сортировать.

Что такое приложения ICA и PCA?

Вы можете использовать ICA для удаления различных видов «шума».

Включение шума в изображение, а также удаление определенных объектов из набора входных данных.

Например, вы можете удалить моргание глаз из данных электроэнцефалограммы. ICA также используется для анализа временных рядов для выявления «трендов».

Это можно применять для прогнозирования цен на фондовом рынке или для анализа тенденций в сообщениях в социальных сетях.

Уменьшение размера данных с помощью PCA можно использовать для визуализации данных.

Вы не можете наносить точки в десятимерном пространстве на двухмерную плоскость экрана.

PCA также можно использовать для сжатия видео и изображений.

Вы можете использовать PCA для подавления шума в изображениях.

PCA также широко используется в:

• Биоинформатика
• Хемометрика
• Эконометрика
• Психодиагностика